几何开始于最简单的图形-直线和圆。
约公元前350年,梅内克缪斯发现了圆锥曲线。
在约公元前250年,佩尔加的阿波罗尼奥斯对圆锥曲线进行首次定义分析。阿波罗尼奥斯对圆锥曲线的构造始于圆和圆心正上方的一个点,用直线连接圆周上的每个点与该悬点,得到的面就是圆锥面。
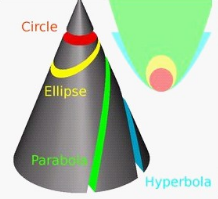
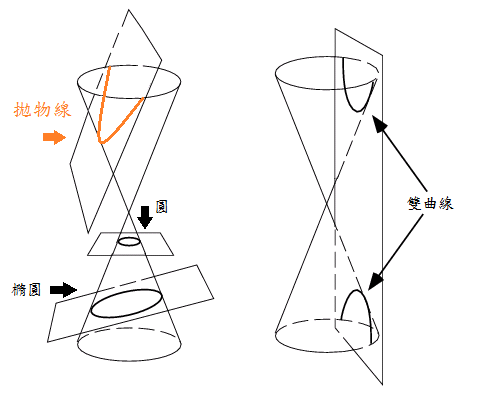
用一个平面去截一个二次锥面,得到的交线就称为圆锥曲线(conic sections)。
圆锥曲线包括椭圆、抛物线、双曲线和圆,通过直角坐标系,它们又与二次方程对应,所以,圆锥曲线又叫做二次曲线。
1 椭圆
圆锥面是最简单的三维图形之一。但是一些复杂的二维曲线包含于圆锥面内。阿波罗尼奥斯的问题是:假设你用一个平面截取那个圆锥圆,截线是什么样?一种可能是,如果正好平行截在恰当的地方,你可以重新得到起初的圆。高一点或低一点,也可得到小一点或大一点的圆。但是当不是平行截取时,出现的图形看起来像是被拉伸或压扁的圆。这就是最常见的圆锥曲线-椭圆。
我们生活的地球每时每刻都在环绕太阳的椭圆轨迹上运行,太阳系其他行星也如此,太阳则位于椭圆的一个焦点上。如果这些行星运行速度增大到某种程度,它们就会沿抛物线或双曲线运行。人类发射人造地球卫星或人造行星就要遵照这个原理。相对于一个物体,按万有引力定律受它吸引的另一物体的运动,不可能有任何其他的轨道了。因而,圆锥曲线在这种意义上讲,它构成了我们宇宙的基本形式。
从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上。
2 抛物线
用一个平行于圆锥的边的平面来截圆锥面,这样生成一条不封闭的“U”形线-抛物线。
我们周围到处是抛物线。如果你向空中斜抛出一块石头,划出的那条轨迹就是抛物线(忽略空气阻力的影响)。抛物线也出现在宇宙中。一些彗星,如哈雷彗星,可预测地、规律性地出现在夜空。也有其它的一些只出现一次的彗星,通常在绕太阳的抛物轨道上运行。
从抛物线的焦点发出的光,经过抛物线反射后,反射光线都平行于抛物线的对称轴。
一束平行光垂直于抛物线的准线,向抛物线的开口射进来,经抛物线反射后,反射光线汇聚在抛物线的焦点。
3 双曲线
通过垂直地切割对顶圆锥使得平面与两个半平面相交来构造这种图形,使得双曲线有两个独立的分支,这两个分支不相交但完全对称-双曲线。
哈勃太空望远镜中的镜面形状就是双曲线,可能让天文学家来观测宇宙。
从双曲线一个焦点发出的光,经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点上。
4 圆锥曲线比较
| 圆锥曲线 | 椭圆 | 双曲线 | 抛物线 |
| 标准方程 | x²/a²+y²/b²=1 (a>b>0) | x²/a²-y²/b²=1 (a>0,b>0) | y²=2px (p>0) |
| 范围 | x∈[-a,a]y∈[-b,b] | x∈(-∞,-a]∪[a,+∞)y∈R | x∈[0,+∞)y∈R |
| 对称性 | 关于x轴,y轴,原点对称 | 关于x轴,y轴,原点对称 | 关于x轴对称 |
| 顶点 | (a,0),(-a,0),(0,b),(0,-b) | (a,0),(-a,0) | (0,0) |
| 焦点 | (c,0),(-c,0)【其中c²=a²-b²】 | (c,0),(-c,0)【其中c²=a²+b²】 | (p/2,0) |
| 准线 | x=±a²/c | x=±a²/c | x=-p/2 |
| 渐近线 | —————— | y=±(b/a)x[4] | ————— |
| 离心率 | e=c/a,e∈(0,1) | e=c/a,e∈(1,+∞) | e=1 |
| 焦半径 | ∣PF₁∣=a+ex∣PF₂∣=a-ex | ∣PF₁∣=∣ex+a∣∣PF₂∣=∣ex-a∣ | ∣PF∣=x+p/2 |
| 焦准距 | p=b²/c | p=b²/c | p |
| 通径 | 2b²/a | 2b²/a | 2p |
